Zcash 是 zk-SNARKs 的第一个广泛应用,zk-SNARKs 是一种新颖的零知识密码学形式。Zcash 强大的隐私保证源于这样一个事实,即 Zcash 中的屏蔽交易可以在区块链上完全加密,但仍然可以通过使用 zk-SNARK 证明在网络的共识规则下验证其有效性。
首字母缩略词 zk-SNARK 代表“零知识简洁的非交互式知识论证”,指的是一种证明结构,在这种结构中,人们可以证明拥有某些信息,例如一个秘密密钥,而无需透露该信息,并且之间没有任何交互证明者和验证者。
“零知识”证明允许一方(证明者)向另一方(验证者)证明一个陈述是真实的,而不会透露超出陈述本身有效性的任何信息。例如,给定一个随机数的散列,证明者可以说服验证者确实存在一个具有该散列值的数字,而无需透露它是什么。
在零知识“知识证明”中,证明者不仅可以说服验证者该数字存在,而且他们实际上知道这样一个数字——同样,无需透露有关该数字的任何信息。“Proof”和“Argument”之间的区别是非常技术性的,我们不在这里讨论。
“简洁”的零知识证明可以在几毫秒内得到验证,即使是关于非常大的程序的语句,证明长度也只有几百字节。在第一个零知识协议中,证明者和验证者必须来回通信多轮,但在“非交互式”结构中,证明由从证明者发送到验证者的单个消息组成。目前,生成非交互式且足够短以发布到区块链的零知识证明的最有效的已知方法是具有初始设置阶段,该阶段生成在证明者和验证者之间共享的公共参考字符串。我们将这个公共引用字符串称为系统的公共参数。
如果有人可以访问用于生成这些参数的秘密随机性,他们将能够创建对验证者来说看起来有效的虚假证明。对于 Zcash,这意味着恶意方可以制造假币。为了防止这种情况发生,Zcash 通过精心设计的多方仪式生成了公共参数。要了解有关我们的参数生成仪式的更多信息,并查看我们为防止暴露 Zcash 所必需的秘密随机性(例如,计算机被喷灯)而采取的预防措施,请访问我们的Paramgen 页面。要了解有关参数生成协议背后的数学原理的更多信息,请阅读我们关于该主题的博客文章或白皮书 ( 1 , 2 )。
如何在 Zcash 中构建 zk-SNARK
为了在 Zcash 中实现零知识隐私,根据网络的共识规则确定交易有效性的函数必须返回交易是否有效的答案,而不会泄露其执行计算的任何信息。这是通过在 zk-SNARKs 中编码一些网络的共识规则来完成的。在高层次上,zk-SNARK 的工作原理是首先将您想要证明的内容转换为关于了解某些代数方程的解的等效形式。在下一节中,我们简要概述了如何将确定有效交易的规则转换为方程,然后可以对候选解决方案进行评估,而无需向验证方程的各方透露任何敏感信息。
Computation → Arithmetic Circuit → R1CS → QAP → zk-SNARK将我们的交易有效性函数转化为数学表示的第一步是将逻辑步骤分解为尽可能小的操作,从而创建一个“算术电路”。类似于布尔电路,其中程序被编译成离散的单步,如 AND、OR、NOT,当程序被转换为算术电路时,它被分解为由加法、减法等基本算术运算组成的单步,乘法和除法(尽管在我们的特殊情况下,我们将避免使用除法)。
以下是用于计算表达式 (a+b)(bc) 的算术电路的示例:
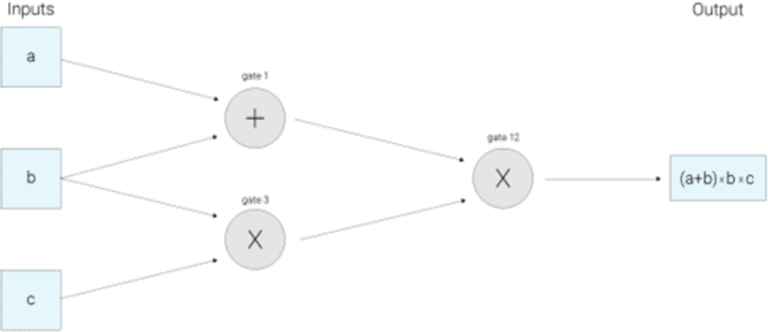
看看这样的电路,我们可以将输入值 a、b、c 视为在电线上从左到右“行进”到输出电线。我们的下一步是构建所谓的 1 级约束系统或 R1CS,以检查值是否“正确移动”。在这个例子中,R1CS 将确认,例如,从 b 和 c 进入的乘法门出来的值是 b*c。
在这个 R1CS 表示中,验证器必须检查许多约束——几乎电路的每条线路都有一个约束。(由于技术原因,事实证明我们只对来自乘法门的电线有约束。)在 2012 年关于该主题的论文中,Gennaro、Gentry、Parno 和 Raykova 提出了一种“将所有这些约束捆绑在一起”的好方法. 此方法使用称为二次算术程序 (QAP) 的电路表示。需要检查的单个约束现在在多项式之间而不是在数字之间。多项式可能非常大,但这没关系,因为当多项式之间不存在同一性时,它在大多数情况下都不会成立。因此,您只需检查两个多项式是否在随机选择的一个点上匹配 以便以高概率正确验证证明。
如果证明者事先知道验证者会选择检查哪一点,他们可能能够制作无效的多项式,但仍然满足该点的身份。与ZK-SNARKs,复杂的数学技术,如同态加密和配对的椭圆曲线的用于评价多项式“盲目地” -即在不知道哪个点正被评估。上面描述的公共参数用于确定将检查哪个点,但采用加密形式,以便证明者和验证者都不知道它是什么。
到目前为止的描述主要解决了如何获得“SNARKs”中的 S 和 N——如何获得一个简短的、非交互式的、单消息证明——但没有解决“zk”(零知识)部分,它允许证明者维护其秘密输入的机密性。事实证明,在这个阶段,通过让证明者使用仍然满足所需身份的原始多项式的“随机移位”,可以轻松添加“zk”部分。
有关 Zcash 中 zk-SNARKs 背后关键概念的分步深入解释,请参阅我们的 SNARKs 解释器系列,其中包含以下帖子:
Zcash 使用bellman,这是一个用于 zk-SNARK 的 Rust 语言库。在 Sapling 升级之前,Zcash 使用了 C++ 库libsnark 的一个分支。要更深入地了解用于 Zcash 的 zk-SNARK 的协议,请参阅有关Pinocchio 协议的论文,该协议一直使用到 Sapling 升级,以及目前使用的Jens Groth 的 zk-SNARK。
如何应用 zk-SNARKs 来创建屏蔽交易
在比特币中,交易通过将发送者地址、接收者地址以及公共区块链上的输入和输出值链接起来来验证。Zcash 使用 zk-SNARKs 来证明有效交易的条件已得到满足,而无需透露有关所涉及的地址或价值的任何关键信息。屏蔽交易的发送者构建了一个证明来证明,很有可能:
- 输入值总和为每个屏蔽传输的输出值。
- 发件人证明他们拥有输入票据的私人消费密钥,从而赋予他们消费的权力。
- 输入票据的私人支出密钥以加密方式链接到整个交易的签名,这样交易就不能被不知道这些私人密钥的一方修改。
此外,屏蔽交易必须满足下面描述的一些其他条件。
比特币跟踪未花费的交易输出 (UTXO) 以确定哪些交易是可以花费的。在 Zcash 中,UTXO 的屏蔽等价物称为“承诺”,花费承诺涉及揭示“无效者”。Zcash 节点保存所有已创建承诺的列表,以及已披露的所有无效者。承诺和无效符存储为哈希,以避免披露有关承诺的任何信息,或哪些无效符与哪些承诺相关。
对于由屏蔽支付创建的每个新票据,都会发布一个承诺,其中包含以下各项的散列:票据发送到的地址、发送的金额、该票据唯一的数字“rho”(后来用于派生无效符)和一个随机随机数。
Commitment = HASH(收件人地址,金额,rho,r)当一个受保护的交易被花费时,发送者使用他们的花费密钥来发布一个无效符,它是来自尚未花费的现有承诺的秘密唯一编号(“rho”)的散列,并提供零知识证明证明他们被授权消费。该散列不能已经在跟踪区块链中每个节点保存的已用交易的无效符集合中。
Nullifier = HASH(支出密钥,rho)屏蔽交易的零知识证明验证了,除了上面列出的条件外,以下断言也是正确的:
- 对于每个输入注释,都存在显露的承诺。
- 无效符和票据承诺计算正确。
- 输出音符的无效符与任何其他音符的无效符发生冲突是不可行的。
除了用于控制地址的支出密钥之外,Zcash 还使用一组证明和验证密钥来创建和检查证明。这些密钥在上面讨论的公共参数仪式中生成,并在 Zcash 网络中的所有参与者之间共享。对于每个受保护的交易,发送方使用他们的证明密钥来生成他们输入有效的证明。矿工通过使用验证密钥检查证明者的计算来检查受保护的交易是否遵循共识规则。Zcash 的证明生成方式需要证明者预先做更多的工作,但它简化了验证,从而将主要的计算工作卸载给交易的创建者(这就是为什么创建屏蔽的 Zcash 交易可能需要几个秒,
Zcash 的屏蔽交易的隐私依赖于标准的、久经考验的密码学(散列函数和流密码),但它是 zk-SNARKs 的添加,与承诺和无效系统一起应用,允许屏蔽交易的发送者和接收者证明加密交易是有效的。为加密货币提供隐私的其他方法依赖于模糊交易之间的联系,但 Zcash 交易可以存储在完全加密的区块链上这一事实为加密货币应用开辟了新的可能性. 加密交易允许各方享受公共区块链的好处,同时仍然保护他们的隐私。计划中的未来升级将允许用户自行决定有选择地披露有关屏蔽交易的信息。有关Zcash 的未来计划,请参阅我们的 Zcash 近期博客文章。
有关如何在 Zcash 中构建屏蔽交易的更深入解释,请参阅我们关于屏蔽地址之间的交易如何工作的博客文章。有关当前 Zcash 协议的完整详细信息,请参阅我们的协议规范。
zk-SNARKs 的未来应用
在 Zcash 中创建屏蔽交易只是 zk-SNARK 的许多可能应用中的一个例子。理论上,您可以使用 zk-SNARK 来验证任何关系,而不会泄露输入或泄漏信息。为复杂函数生成证明仍然是计算密集型的,对于许多应用程序来说不实用,但Zcash 团队正在推动优化 zk-SNARKs 的边界,并且已经通过更有效的实现开辟了新天地。
就目前而言,Zcash 的 zk-SNARK 实现可以添加到任何现有的分布式账本解决方案中,作为企业用例的零知识安全层。Zcash 团队的科学家是世界上最博学的 zk-SNARKs 研究人员之一,并不断致力于提出新的应用程序并提高零知识协议的效率。如果你的业务需要,可以从零知识证明或具有强大的隐私blockchain应用的解决方案中受益,取得联系我们的业务发展团队。
原文:https://z.cash/technology/zksnarks/
版权属于:区块链中文技术社区 / 转载原创者
本文链接:https://www.bcskill.com/index.php/archives/1192.html
相关技术文章仅限于相关区块链底层技术研究,禁止用于非法用途,后果自负!本站严格遵守一切相关法律政策!